BJT Amplifier
This page talks about how to design a simple BJT common emitter amplifier. Below are the full derivations for component values because I CBA to work this out every time some fellow student asks me to explain this after they fail the EE exam ;) Thanks to the professor who can't explain this clearly enough on the lecture for the n-th year.
Contents
Task
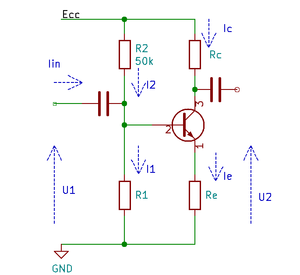
Below is an NPN common emitter amplifier. Design the elements so that
- Collector current Ic = 1mA
- Collector-emitter voltage Uce = 6V
- Voltage gain for the AC component Ku = ΔU2/ΔU1 = 23
- Current for resistors R1 and R2 is much larger than the base current
- Supply voltage Ecc = 12V
Transistor parameters:
- Current gain beta=200 (also called hfe)
- Base-emitter voltage drop Ube0 = 0.66V
- Input impedance h11 = 500R
- Assume R2 = 50k
Calculate the input impedance rin = ΔU1 / ΔIin
Rc and Re
The problem is formulated in a way that requrement 3 is actually step one. This circuit is a common emitter amplifier, it's Ku = Rc/Re. This gives us a constraint for Rc and Re, that is
Rc/Re = 23 Rc = 23Re
Additionally there's requirement #2, that is Uce = 6V. Note that this is half of the supply voltage and that's how these are usually designed for maximum swing. From these two constraints we can calculate Re and Rc. Here's how
We have to take a look at the Rc-C-E-Re branch of the circuit (right vertical). The volage on it is Ecc=12V. The Uce voltage is 6V. This leaves us with 6V to "split" between Rc and Re. The voltage drops are
IcRc + Uce + IeRe = 12V IcRc + 6V + IeRe = 12V IcRc + IeRe = 6V
Because the beta is large (200), then Ie ~= Ic (this is because Ie = (beta+1)*Ib, Ic = beta*Ib ). From requirement #1 we get
Ic(Rc+Re) = 6V Rc + Re = 6V/Ic = 6kohm Rc = 23Re 24Re = 6k --> Re = 0.25k, Rc = 5.75k
R1 and R2 (biasing voltage divider)
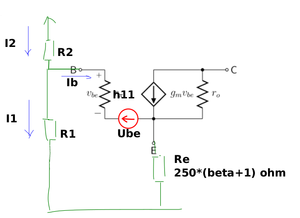
We have to look at the R2-R1 branch and the bottom part of the right branch, B-E-Re. Transistor's h11 is also given, so we have to include it in the calculation. For that we need the hybrid-pi model
Calculating the bias is finding what voltage at the base to get the necesary Ic (~= Ie) current. We have to find a value of Ub so that the right Ib = Ic/beta flows through h11 and (beta+1)*Re in series.
Ib = Ic/beta Ub = Ib*h11 + Ube + Ib*(beta+1)*Re Ub = Ic*h11/beta + Ube + Ic*(beta+1)/beta*Re
For a large enough beta (200), the term (beta+1)/beta is practically 1.
Ub = Ic*h11/beta + Ube + IcRe Ub = Ic(h11/beta + Re) + Ube
Re = 250R, h11/beta = 500R/200 = nothing, so we ignore it. But you have to write this on the exam to show that you know the Hybrid Pi model ;)
Ub = IcRe + Ube Ub = 1mA * 250ohm + 0.66V Ub = 0.91V
Now for R2 = 50k we have to pick R1 so that we get a voltage divider with a specified output voltage. Note that we have to include the load of h11 + Re*(beta+1) in parallel with R1. We do this by finding the currents.
I2 = (Ecc-Ub) / R2 I1 = I2 - Ib R1 = Ub/I1 R1 = Ub/([Ecc-Ub]/R2 - Ib) R1 = Ub/([Ecc-Ub]/R2 - Ic/beta) R1 = 0.91V / ([ 12V - 0.91V] / 50kohm - 1mA/200) R1 = 4197 ohm
Watch out for the units. If R1 comes out negative, you screwed the units up.
Input impedance for AC
zin = ΔUin/ΔIin
ΔUin = ΔUb. There is nothing tricky here, for AC analysis the capacitor is a short.
Iin + I2 = I1 + Ib ΔIin + ΔI2 = ΔI1 + ΔIb
ΔI2 = (Ecc-Ub)/R2. For AC analysis the AC component of the supply voltage is zero (for AC analysis we treat all supply rails as ground)
ΔI2 = -Ub/R2
Do not forget about that minus.
In a similar vein
ΔI1 = ΔUb/R1
Now we have to find ΔIb. From the image above
Ib = Ub/(h11 + Re*[beta+1])
Deltifying that equation yields
ΔIb = ΔUb/(h11 + Re*[beta+1])
Putting all the equations together
ΔIin = ΔI1 - ΔI2 + ΔIb ΔIin = ΔUb/R1 + ΔUb/R2 + ΔUb/(h11 + Re*[beta+1])
Watch out for signs. Here ΔUb/R2 has a plus because ΔI2 is taken with a minus. This matches because as I said, for AC we treat the power rails as grounds, so R1 is in paralell with R2 and hence the 1/R1 + 1/R2 term.
zin = ΔUb/ΔIin = ΔUb / ( ΔUb/R1 + ΔUb/R2 + ΔUb/(h11 + Re*[beta+1]) ) zin = 1/( 1/R1 + 1/R2 + 1/(h11 + Re*[beta+1]) )
This is the input impedance.
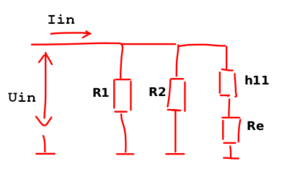
Of course this is the academic approach. The above zin equation can be found immediately, by drawing a clever schematic...
Schematic for the AC analysis
A clever engineer will notice that the input impedance is just three impedances in parallel: R1, R2 and h11+Re.
zin = R1 || R2 || (h11+Re)
Practical build tips
If you are actually building something like that, the fastest way to do so is:
- Pick Re and Rc so that Re is a nice and round E24 value in the 1k-10k range
- As you can see, for a large enough beta (nowadays any transistor), the h11/beta term disappears, so Ub = IcRe + Ube
- For the same reason, if Re is like above, then Ic/beta is also small so you can just ignore it and suppose the R1-R2 divider is unloaded
In practice any errors caused by the above assumptions are probably smaller than errors caused by using E24 resistors with 5% tolerance. And that amplifier is not temperature compensated anyway, so if you open a window in the lab and some cold air blows on it, the gain's gonna change.
PNP amplifier
An experienced engineer is CBA to calculate all of that again. Just swap the transistor for a PNP and swap the power rails.